1. Taxonomy Tables

Samplers (ComfyUI) – Each sampler defines how to integrate the denoising ODE/SDE:

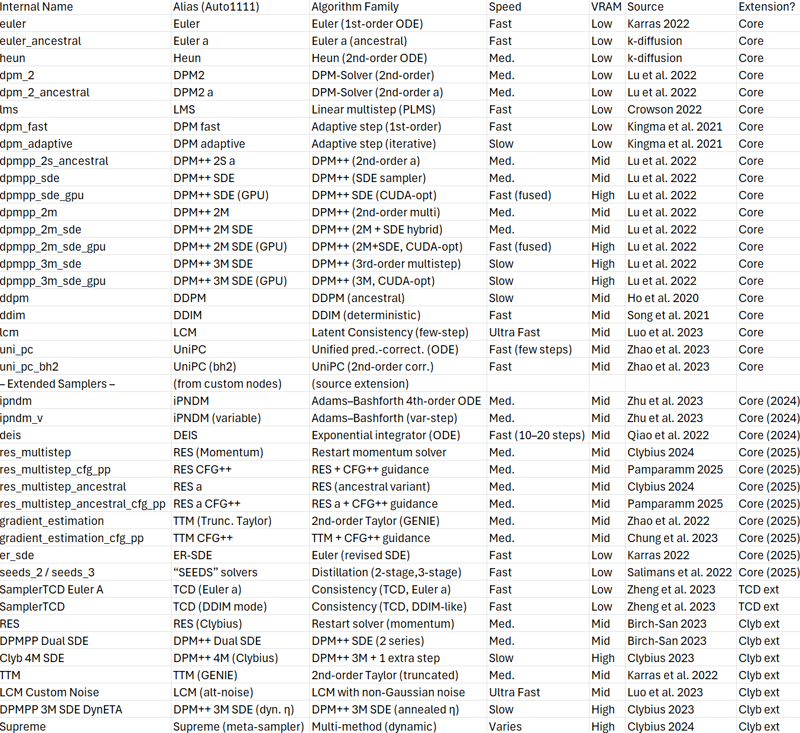
1.   Algorithm Deep-Dive

Samplers (Mechanics & Origins)

• Euler – A classic 1st-order explicit solver for the diffusion ODE. Each step simply predicts noise ε and subtracts it: x_t-Δt = x_t - ε_θ(x_t, t). Introduced via Karras’s sampler suite (k-diffusion), it’s very fast but can leave residual noise/artifacts. Strength: speed and simplicity – great for quick drafts or when few steps are needed. Weakness: less accuracy on fine details (may require ~20+ steps for convergence). Euler is deterministic and converges reliably as steps increase, making it a robust baseline sampler.

• Euler a – The “ancestral” Euler adds random noise at each step. This stochastic sampler injects a bit of fresh noise after denoising, preventing strict convergence. Originating from Latent Diffusion (original PLMS sampler) and k-diffusion’s Euler a, it produces more diverse, “dreamy” outputs. Strength: can yield more creative or vivid results due to randomness reintroductions – often favored for artistic or anime styles to avoid looking too “clean.” Weakness: Non-convergent – images won’t stabilize even at high step counts, and final quality can plateau or even degrade with excessive steps (fine details get washed by added noise). Not ideal for reproducing the exact same image with more steps (since outcomes vary with step count).

• Heun – A 2nd-order Runge–Kutta method (also known as improved Euler). At each step, Heun does a preliminary Euler prediction and then a correction using the new derivative. In practice, it samples noise twice per step: once for a trial move, then refines the latent with a trapezoidal rule averaging. Source: Karras et al. (2022) introduced Heun in their diffusion sampler family. Strength: Higher accuracy and faster convergence than Euler – often reaches a given image quality in ~2 fewer steps. It’s known to produce cleaner details at lower step counts. Weakness: ~2× slower than Euler (it calls U-Net twice per step), so Heun@30 steps  Euler@15 steps in compute. It shares Euler’s deterministic nature (converges steadily) but requires more VRAM/time. Good for when quality is needed but speed is less critical.

LMS (PLMS) – A linear multistep deterministic solver derived from the original Pseudo Linear Multistep method used in Stable Diffusion v1. Instead of one-step prediction, LMS uses a history of previous steps to extrapolate the next latent. It was introduced by Stable Diffusion authors (LDM, 2022) as an faster alternative to DDIM. Strength: Faster convergence than Euler at similar cost by reusing past gradients; good at maintaining stability and structure (less flicker). Weakness: In practice, LMS in ComfyUI can struggle with certain schedules – e.g. LMS Karras sometimes stalls at a higher residual error. It may also produce slightly oversharpened or high-contrast outputs compared to Euler. LDM’s own tests showed PLMS sometimes underperformed DDIM in fine details. Today it’s considered a bit “old-school” and has largely been surpassed by DPM++ solvers.

DDIM – Denoising Diffusion Implicit Models, introduced by Song et al. (2020), is a first-order deterministic sampler that treats diffusion as a non-Markovian process. It deterministically maps the noise through time steps, allowing much faster sampling (~10–50× fewer steps than DDPM). Strength: Very stable and preserves image consistency – it was one of the first samplers enabling decent images in ~50 steps instead of 1000 7 . DDIM also enables latent interpolation and one-click “noiseless” generation (when steps). Weakness: Lower diversity (no stochasticity) – tends to always produce the same result for a given seed and prompt, which can be a downside for creative exploration. In fact, images can look a bit blurry or smooth compared to solvers that add stochasticity or higher-order corrections. Often used when reproducibility is needed or as a starting baseline.

• PNDM – Pseudo-Numerical Diffusion Methods, by Liu et al. (2022), is a higher-order technique building on DDIM. It essentially applies a 4th-order multistep method (analogous to Adams–Bashforth) in latent space. PNDM was implemented as “PLMS” in early Stable Diffusion releases and can generate quality images in ~50 steps (20× faster than naive DDPM). In ComfyUI, PNDM’s legacy lives on as LMS and DPM2 a samplers. Strength: faster convergence than DDIM, retaining quality with fewer steps (it was key to SD1.x’s speed-up). Weakness: The method can overshoot or produce minor artifacts if step count is too low (due to error accumulation in high-order integration). Modern DPM++ solvers have refined this approach further (addressing some instability).

DPM2 / DPM2 a – These samplers come from DPM-Solver by Lu et al. (2022). “DPM2” indicates a second-order solver; the ancestral variant adds noise each step. They solve the diffusion ODE with higher order discretization, achieving good quality ~2× faster than Euler or DDIM (since error scales with step² instead of step). DPM2 a (sometimes likened to PLMS) introduces randomness, giving non-convergent but often aesthetically pleasing results. Strength: More accurate than first-order methods; DPM2 converges better than Euler/Heun when using smaller step counts 1 . It tends to preserve fine structures and geometry well. The a version (ancestral) yields a bit of extra texture and variation, handy for certain styles (but lacking reproducibility). Weakness: As 2nd-order solvers, they take 2× compute per step, and DPM2 a shares the non-convergence drawback of ancestral samplers. These were cutting-edge in late 2022, but now often overshadowed by DPM++ improvements 11 .

DPM++ 2S a – Diffusion Probabilistic Model Solver++ (two-step, ancestral) is a Karras-improved sampler introduced in mid-2022 10 . It’s essentially a two-stage solver (like DPM2) but with an extra noise correction, and “ancestral” indicates adding noise each sub-step. Popularized via k-diffusion and Automatic1111 (the “DPM++ 2S a” option). Strength: Excellent detail and arguably one of the topquality samplers for difficult textures. Users often report DPM++ 2S a yields the sharpest results among ancestral samplers, at the cost of more steps. It particularly shines with Karras scheduling (often labeled “DPM++ 2S a Karras”) – in fact, one user calls it the best quality sampler if you don’t mind the speed hit. Weakness: Slow (2 U-Net evaluations per step) and non-convergent. It may produce high-fidelity detail but with slight flicker – e.g. small changes in step count or CFG might alter the output significantly. Best used when you lock a seed/steps and want maximum quality.

DPM++ SDE – A solver treating the reverse process as an SDE (Stochastic DE), as described by Karras et al. in Elucidating Diffusion 10 . It adds controlled noise at each step proportional to the diffusion schedule. ComfyUI’s DPM++ SDE (from Karras/Crowson code) yields highly realistic textures and is stochastic (even without “a” in name, it behaves randomly due to the SDE term). Strength: Very good at photorealistic effects and fine details – it was found to produce “crisp and detailed” images given enough steps. It particularly excels with small step sizes; the Karras SDE variant is known for highquality samples in 15–20 steps for guided SD models. Weakness: Does not converge if steps increase – much like ancestral samplers, the image can keep changing (even degrading past some point). The output can “fluctuate significantly as the number of steps changes”. Also, because it injects noise, it can introduce grain or instability on very low steps if not paired with an appropriate schedule. In summary, DPM++ SDE is powerful for realism at moderate step counts, but one must treat it as a stochastic sampler.

DPM++ 2M & 3M – These are multistep solvers introduced in DPM-Solver++ v2. “2M” uses a secondorder Adams-Bashforth approach but with a twist: it keeps two previous denoised states (hence 2M) and applies a momentum correction. “3M” similarly uses three past states (third order). They were designed to improve stability at higher guidance scales. Strength: DPM++ 2M is widely regarded as one of the best all-around samplers for Stable Diffusion. It converges quickly, produces sharp details, and handles high CFG well (especially the Karras version). Many users report it balances speed and quality optimally. DPM++ 3M can surpass 2M in quality for very high step counts or tricky cases, but… Weakness: 3M often needs more steps to show benefits (it’s higher order, so low-step usage can be unstable or overkill). In practice, 2M Karras with ~20–30 steps often outperforms 3M with the same steps. Both 2M and 3M are deterministic (no randomness), so they converge as steps increase. However, if used with an unsuitable scheduler, they can “overshoot” (e.g. 2M with a too-aggressive schedule might produce overly contrasty or weird results – see Compatibility). Generally, DPM++ 2M Karras became the default recommendation for photorealistic generations in SD1.5 and SDXL.

UniPC – A Unified Predictor-Corrector sampler by Zhao et al. (2023). It combines both ODE solvers and SDE correctors in a single framework and was shown to generate high-quality images in as few as 5–10 steps 8 . UniPC’s algorithm adaptively switches between predictor (denoise guess) and corrector (adjust with noise) using model-specific criteria. It also introduced a special “bh2” 2ndorder correction variant (Comfy’s uni_pc_bh2 ). Strength: Extremely fast convergence – it often achieves near-optimal quality with very low step counts, which is why Stability AI adopted it for SDXL in some settings. It’s also designed to handle strong CFG (Classifer-Free Guidance) without divergence, addressing instability issues that earlier solvers had at high CFG. Weakness: Slightly slower per step (the predictor+corrector means extra computations; bh2 doubles up steps in parts). Also, it may be a bit less intuitive to tune – some schedules might not pair obviously (the authors suggest using their time-uniform or a tailored step size sequence for best results). In ComfyUI, UniPC is deterministic and tends to be robust; any quality gap versus DPM++ is small, and with enough steps it can match others. Its strength really shines in low-step scenarios or when trying to squeeze maximum quality out of ~5–10 steps runs.

IPNDM – The Improved PNDM implemented in 2024 (in ComfyUI core) is essentially a 4th-order Adams-Bashforth method for diffusion, plus a variant with variable step sizes. It was inspired by research on higher-order solvers and the observation that PNDM’s original formulation assumed uniform step intervals. The ipndm sampler keeps step sizes equal (like original), whereas ipndm_v adjusts coefficients for non-uniform step spacing. These were contributed by open-source developers (noted by zhyzhouu on GitHub) referencing numerical analysis literature. Strength: As a 4th-order solver, IPNDM can in theory converge in even fewer steps than 2nd or 3rd order methods, and handle complex scenes with less noise. Some community tests found IPNDM can produce slightly more vibrant or detailed results at high steps (50+) compared to 2M. Weakness: At low step counts (e.g. 10–20) it showed only marginal gains and sometimes performed worse than 2M (perhaps due to error accumulation when guidance is high). Also, it’s computationally heavier (4th order means 4 evaluations per step, though some optimizations may reuse work). It remains somewhat experimental – one developer noted the fixed-step version empirically worked better than the variable-step in tests. In sum, IPNDM is a promising high-order solver, but benefits mostly seen in niche cases (small resolutions or very high quality demands).

• DEIS – Fast Sampling of Diffusion Models with Exponential Integrator by Qiao et al. (2022). DEIS is a solver that applies an exponential integrator technique to the diffusion ODE, which allows larger step sizes by analytically integrating the linear part of the SDE. ComfyUI added DEIS (order 3) in mid-2024. Strength: DEIS can achieve high-fidelity samples in as low as 10 steps. It was shown to outperform DDIM and even compete with DPM-solvers in low-step regimes. Users have noted DEIS gives amazing results fast – one Redditor was “surprised this sampler is not talked about more”. Because it explicitly handles the linear noise decay, it can preserve colors and contrast better at low step counts. Weakness: DEIS may require an appropriate scheduler; the authors recommended a time-uniform or SNR-based spacing for stability. If used with a poor schedule, it can generate oversaturated or distorted images. Also, at higher step counts (50+), its advantage diminishes as other high-order solvers catch up. In practice, it’s a go-to for quick drafts when one wants more quality than Euler but still fewer steps than DPM++ requires. Notably, Diffusers library has a DEIS sampler implementation confirming its speed/quality trade-off.

• RES (Restart) – “RES” is a custom sampler by community devs (Birch-San, Kat, Clybius) that introduced a momentum restart concept. It’s essentially Euler or Heun with an added momentum term that periodically resets (or “restarts”) to avoid getting stuck in bad local minima. The implementation naively adds a momentum buffer to the latent and can improve sharpness. Strength: Can yield sharper and more detailed images at the same step count by reusing part of the previous step’s change (like an Nesterov momentum in optimization). Particularly effective for highfrequency details or when pushing for very few steps. Weakness: It’s somewhat experimental – described as “somewhat naively momentumized” by its author. If momentum is too strong or schedule too gentle, it might overshoot and cause speckle or detail artifacts. Also, not a standardized method from literature (though momentum methods for diffusion have been explored in papers like PNDM and GDDIM). ComfyUI later integrated a refined version “res_multistep” with CFG support, indicating the approach showed merit.

• TTM (Truncated Taylor) – TTM sampler stems from the paper GENIE (Higher-Order Diffusion Solvers via 2nd-order Taylor expansion) by Wang et al. (NVIDIA, 2023). It uses a truncated Taylor series to solve the diffusion ODE, effectively a 2nd-order method but derived differently than standard solvers. Clybius added a custom TTM node referencing that work. Strength: It can capture some higher-order effects with potentially fewer function evaluations. GENIE’s truncated Taylor (called “TTM”) was shown to improve stability for large steps and helped produce high-quality samples with fewer iterations in their experiments. In practice, TTM in ComfyUI is a bit niche – one would use it in scenarios similar to DPM2 or Heun. Weakness: If the model’s dynamics don’t match the Taylor assumptions, it can be “mathematically unsound (but fun!)” as one extension author put it. Essentially, truncating at 2nd order can lead to slight instability unless step sizes are small. It’s not widely used compared to DPM++, and might require careful scheduling to truly shine. Consider it an alternate 2nd-order solver that’s still experimental.

LCM (Latent Consistency Model) – Not a traditional sampler but a special one-step (or few-step) model inference technique. LCMs (Luo et al., 2023) fine-tune the diffusion model to jump directly from random noise to image in a handful of steps. In ComfyUI, enabling lcm sampler means you’re using a model (or LoRA) trained for consistency, and the sampler will only take ~4–8 steps with a custom schedule. Under the hood, the “sampler” is trivial (often just one DDIM-like step), but the model has extra weights to make this work. Strength: Speed – one can generate a reasonably good image in 1–4 denoising steps if the LCM LoRA is applied. It’s essentially ~10× faster sampling for a slight quality trade-off. It’s also great for animation or real-time applications where diffusion would normally be too slow. Weakness: Requires a dedicated LCM-trained model or LoRA; you must use the LCM sampler with the LCM weights – otherwise images are just noise. Also, quality can be lower or differ in style from standard SD (images may appear smoother or less detailed, due to the model compressing the generation into fewer steps). When an LCM LoRA is loaded, Comfy’s KSampler node switches to an “LCM mode”; using any other sampler yields black or noisy outputs. In summary, LCM sampler is a special case – incredibly fast drafts, but model-dependent.

• Supreme – This isn’t a single algorithm, but a meta-sampler node from Clybius’s extension. The Supreme sampler exposes many tweakable options: dynamic step order, centralization (subtract mean), normalization, edge enhancement, noise modulation, etc.. Under the hood, it can behave like Euler, DPM2, RK4, or even an adaptive RK45 depending on settings. It also implements reversible sampling (a technique from TorchSDE and recent research) where latent updates can be partially reversed to preserve information. Strength: Ultimate flexibility – one can experiment with advanced ideas (e.g. add a bit of frequency noise modulation to sharpen textures, or use substeps to iterative refine each step). The Supreme sampler can yield higher quality at same steps by using Dynamic mode (adapts order based on error, up to RK45). Weakness: Very complex to tune – many settings can degrade image or cause odd color shifts if misused (the documentation warns “There be dragons” with extreme values). It’s also heavier on compute if you crank up substeps or high-order modes. Supreme is great for power users who want to squeeze every drop of quality or try experimental solvers (like Bogacki-Shampine 3rd order or reversible Heun), but it’s not a plug-andplay improvement for casual use. Its results are only as good as the user’s understanding of those techniques – truly a sandbox for diffusion researchers and enthusiasts.

Schedulers (Noise Schedules & Step Spacing)

Linear (“normal” β-schedule) – The default noise schedule from the original DDPM paper (Ho et al. 2020) uses a linear increase in β over steps 6 , which translates to a roughly linear decrease in noise variance each step. ComfyUI’s normal scheduler closely matches this, removing a fixed fraction of noise per step. In practice, it’s a good all-purpose schedule that was used to train Stable Diffusion 1.x models. It spends steps evenly across the diffusion timeline. Strength: Simplicity and broad compatibility – all samplers will produce usable results on a linear schedule. It doesn’t emphasize any part of the process disproportionately, so it’s stable. Weakness: Not optimally efficient – early steps might waste time on high noise, and late steps might remove too much too quickly. Newer schedules (Karras, etc.) outperform linear in detail retention. Nonetheless, linear remains a safe default, especially for deterministic samplers where one wants predictable behavior akin to training.

Karras – Karras et al.’s 2022 work introduced a noise schedule that distributes steps in a sigmoidlike fashion: very small step sizes near the end (to carefully approach the final denoise) and larger steps earlier (to quickly traverse high-noise regions). ComfyUI’s karras scheduler implements this “η=1” schedule from the paper, often referred to as sigma or ρ-schedule. Strength: Significantly improves final image quality at low step counts – by spending more steps where it matters (low noise), it preserves details and reduces late-stage artifacts. It’s known to yield cleaner, sharper results especially when combined with advanced samplers like DPM++ 2M or SDE. Many users observe that Karras variants converge faster – e.g. DPM++ 2M Karras might need only 20 steps where normal needs 30 for similar quality. Weakness: Can be incompatible with some ancestral samplers – because it prolongs the end (where noise is small), an ancestral sampler will keep injecting noise in those tiny steps, leading to grain or non-convergence. Indeed, using Karras with Euler a or DPM++ SDE often yields slightly noisier outcomes than a linear schedule would (they “overshoot” by adding noise in micro-steps). Also, Karras assumes infinite continuum of steps; at very low step counts (5) it can sometimes underperform simple schedules since the early large steps skip too much. Overall, though, for most samplers that converge, Karras is highly recommended for quality.

Exponential – An exponential sigma schedule spaces noise values geometrically. For instance, each step might remove a fixed percentage of the remaining noise. In ComfyUI exponential scheduler, the noise level σ might follow σ_i=σ_max(σ_min/σ<sub>max</ sub>)^(i/(N-1)). This means early steps remove very little noise (if σ is high) and later steps remove a lot. The effect: images tend to have clean backgrounds and smooth gradients 9 , as the schedule spends more time in high-noise regime refining global features, then rapidly clears out noise at the end. Strength: Good for scenarios where backdrop clarity is key – e.g. landscape skies, uniform areas, or preventing early detail formation that could become muck. It often pairs well with multi-step samplers like 2M/3M to counteract their tendency to oversharpen; exponential spacing “softens” the progression. Weakness: Can lose fine details because the final steps are very large – details might be washed out as noise plummets. Also, if a sampler already injects randomness (ancestral), exponential can make results less predictable* (big final leaps + noise can jumble small features). Typically, this schedule is slightly less popular than Karras or linear, but some SDXL workflows noted exponential works nicely with 3M samplers to maintain coherence. It’s something to experiment with if Karras yields too much micro-detail or takes too long in final steps.

Simple (Uniform) – The simple scheduler in ComfyUI uses uniform step spacing in time t (diffusion time). Essentially, if total steps N, each step jumps an equal amount of the diffusion timeline. In continuous terms, it’s like an approximately quadratic fall-off in noise (since early t corresponds to high noise %). It’s very similar to the “linear” schedule for small σ, and to exponential for large σ – a middle ground. Strength: Reliable and straightforward – like linear, it’s broadly compatible and doesn’t weight too heavily on any section. Many community workflows still default to simple for ease. It can be thought of as time-linear vs. noise-linear. Weakness: Not particularly optimized – it doesn’t leverage the insight that denoising benefits from smaller steps at the end. So image quality might be a bit lower at identical step count versus Karras (which is why Karras schedules are preferred in many comparisons). Still, simple/uniform is useful as a baseline and is sometimes used in testing sampler implementations to avoid any schedule bias.

DDIM Uniform – This schedule evenly spaces steps in the alpha (or (1-α) ) domain used by DDIM. In other words, it mirrors how DDIM would choose time intervals if asked for N steps (basically t_i = i(T/ N)). It’s included to match the exact behavior of DDIM and related deterministic samplers. Strength: Ensures that DDIM sampler outputs match those from other UIs* (like Automatic1111) when using “DDIM” – which is helpful for reproducibility and validation. It’s also conceptually simple. Weakness: For other solvers, using ddim_uniform might not make much difference from simple or linear. It’s largely there for compatibility. One might choose this scheduler if they specifically want to mimic the training trajectory of diffusion (as DDIM is derived from the analytic DDPM inversion which assumes uniform time).

Karras (SGM) Uniform – Labeled sgm_uniform , this schedule aims for uniform spacing in terms of scaled sigma or SNR (signal-to-noise ratio). It’s inspired by Score SDE methods (Song et al.) where a VE (variance-exploding) SDE often uses uniform discretization for predictor-corrector schemes. In practice, it means early steps are closer together in t (since σ is high, SNR low) and later steps more spread, opposite to Karras’s sigma spacing. Strength: Potentially useful for samplers that have an internal PC mechanism (like UniPC or IPNDM), where maintaining a roughly constant SNR per step can stabilize the corrector step. It may also benefit consistency or distillation-based models (which Trajectory Distillation might prefer – though TCD uses its own scheduler). Weakness: Not commonly used in user workflows – it’s somewhat esoteric. If used with regular samplers, it might produce results similar to an exponential or even linear schedule (depending on interpretation). It’s included likely for completeness and to allow advanced users to try matching academic schedules from certain papers (the name SGM suggests Score-based Generative Model uniform schedule).

Beta (β) Scheduler – This refers to the family of schedules parameterized by α and β exponents as described in Karras et al. Appendix. ComfyUI’s beta_1_1 in PPM extension explicitly sets both exponents to 1.0, resulting in a pure linear schedule in noise and time. The default normal might use α1, β1 (slight curvature). The ability to tweak these can yield custom curves. Beta_1_1 specifically is a straight-line in noise space (if you plot σ vs step, it’s linear). Strength: Sometimes a linear schedule is all you need and avoids any bias – beta(1,1) is essentially the simplest schedule. If any fancy schedule causes issues, beta_1_1 will be the fallback that mimics original stable diffusion’s intent. Weakness: Without knowing the underlying α,β of “normal”, it’s hard to say how different 1.0,1.0 is – likely “normal” was already near-linear (some implementations use β_start=0.00085, β_end=0.012 for 1000 steps in DDPM). The PPM extension provided this mostly for completeness or testing. Few users manually pick beta_1_1 unless troubleshooting. It’s essentially “linear schedule, guaranteed”.

Align Your Steps (AYS) – A custom scheduler introduced by community members (Extraltodeus, Koitenshin). It attempts to “align” the noise schedule with how SDXL was trained. Specifically, SDXL training reportedly emphasized certain timesteps (perhaps mid-range) – AYS modifies the sigma curve to match that distribution. The ComfyUI-ppm extension provides ays (SDXL variant) and ays+ (which forces final sigma to min). Strength: For SDXL models, AYS can improve consistency and detail, especially at standard step counts (~30). It essentially acts like a midpoint-focused Karras: more steps in mid-noise range to refine anatomy and comp, but also enough at end (AYS+ ensures end at exactly sigma_min). Users of SDXL have reported that AYS yields better results than vanilla Karras in some cases – a known SDXL issue is the “0 sigma” end noise, which AYS+ addresses by avoiding too abrupt an end. Weakness: It’s heuristic; not derived from first principles. On non-SDXL models, it may or may not help (it was modified by Extraltodeus for SDXL’s noise scaling). Also, using AYS schedules might require a matching sampler (one user noted AYS+ with high steps can still lead to dark or saturated images if the sampler isn’t tuned). Essentially, it’s a tailor-made schedule – great if it matches your model’s needs, otherwise uncertain.

GITS / AYS-30 – These are further custom schedules from Koitenshin’s experiments (the name “GITS” possibly shorthand they chose). ays_30 is a variant presumably optimized for 30 steps runs, and gits might be another curve or an experimental scheduler. Without official documentation, we infer: they are based on Align Your Steps 32 from Koitenshin, likely providing an alternate step spacing for specific step counts. Strength: Might squeeze extra quality at fixed step counts (e.g. if you must use 32 steps, AYS_32/GITS could allocate them ideally). Weakness: Niche and possibly unstable outside their intended settings. These schedules replace the internal sigma function via monkey-patching – so one should use them only if they know the context (e.g. a known workflow recommends it). As they are in PPM “hooks”, we mark them experimental.

TCD Scheduler – From Trajectory Consistency Distillation (M. Zheng et al., 2023). In TCD, the model is trained such that a few large denoising jumps yield a good result, by enforcing consistency between long and short trajectories. The TCDScheduler in ComfyUI allows using those large jumps: e.g. 4 steps that would normally correspond to 50 steps of DDIM. It’s essentially a non-uniform schedule where each step is huge (t spacing determined by the TCD algorithm). Strength: When using a TCDdistilled model, it enables lightning-fast sampling (similar spirit to LCM, but via distillation). For instance, the authors demonstrate 6-step trajectories that match 50-step DDIM quality. The scheduler ensures each step’s γ (see below) is applied correctly to maintain the consistency. Weakness: Only relevant if model supports it – applying TCDScheduler to a regular model = likely poor output (it’s like doing only 4 DDIM steps on an undis tilled model – very under-sampled). It’s a specialized tool. The TCD extension notes that currently the WIP sampler “SamplerTCD” is just a DDIM stub, so effectively one should use SamplerTCD Euler A with TCDScheduler for now. In summary, TCDScheduler is part of an emerging approach to accelerate diffusion using consistency models; promising, but model-dependent.

LCM Scheduler (γ) – A special scheduler introduced alongside TCD in the extension, but conceptually for blending deterministic and stochastic sampling. It has a parameter γ that “acts as a sort of crossfade between Karras and Euler”. When γ=0, you get a deterministic schedule (like Euler or perhaps linear); γ=1 gives fully stochastic (like an ancestral/Karras). Values in between mix the noise contribution. Strength: Allows fine-tuning the trade-off between determinism and randomness per step. For example, one might use γ0.3 (default) to add a bit of randomness so the sampler explores more, but not so much to derail convergence. Increasing γ for more steps is recommended (to keep introducing variety as the model has more chances to refine). This is a novel idea not present in core samplers – effectively a partial ancestral scheduler. Weakness: Only works with samplers aware of it (TCD’s SamplerTCD uses it). It’s also an extra hyper-parameter for the user to worry about, and might confuse results if not understood. Think of it as blending two extremes: one end you get a clean but possibly less diverse output, the other you get a very stochastic path. The optimal γ may depend on step count and model; the extension suggests higher γ for more steps. This is an advanced tool for power users seeking to tweak noise influence.

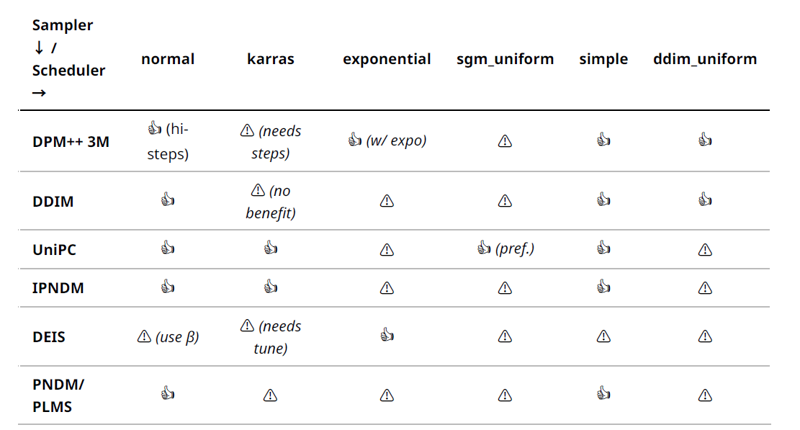
2.   Compatibility & Combo Matrix

Sampler vs Scheduler Compatibility: The table below rates each sampler–scheduler pair: 👍 Recommended,  Use Caution , or  Not Advised. These ratings reflect community experiments and known theoretical stability. (Core samplers listed; extensions often have fixed pairings.)

Legend: Rows = Samplers, Cols = Schedulers. 👍 = proven stable & high quality;  = works but potential issues (quality or stability);  = known incompatibility or poor results.

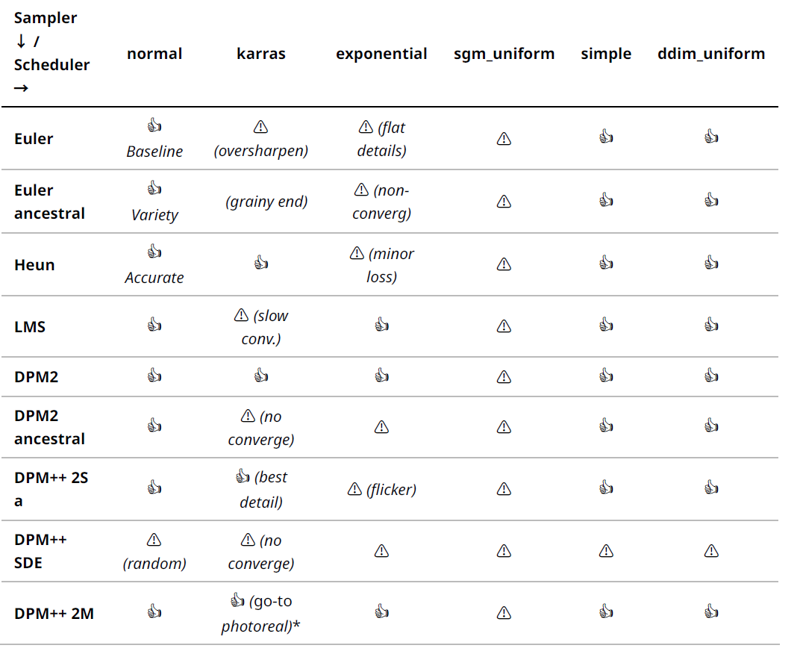
• DPM++ 2M Karras – Photoreal workhorse: This combo is widely praised for sharp, clean outputs with fewer steps. It retains fine details even at 20 steps and handles high resolutions well. Rationale: Karras schedule finely resolves late-stage noise, and DPM++ 2M’s accuracy preserves textures – ideal for SDXL and realistic styles (e.g. keeps sharp edges and coherent lighting in portraits).

• DPM++ 3M Exponential – High-res stability: Users found DPM++ 3M benefits from an exponential schedule to distribute effort earlier. It produces very stable large images (2K+ upscales) since the expo schedule cleans backgrounds gradually while 3M solver maintains structure. Rationale: 3M needs more steps; exponential ensures it doesn’t waste them all at the end – great for upscaling pipelines where coherence is crucial (no sudden detail shifts).

• Euler / Heun with normal/simple – Baseline and balanced: Euler + normal (or simple) is the reference for consistency – always reliable for drafts or testing (no scheduler trickiness). Heun + Karras is another sweet spot: Heun already converges faster, and Karras further improves detail in final steps – often recommended for medium steps (e.g. Heun Karras ~20 steps can match Euler 30 in quality while being deterministic).

UniPC with SNR uniform – Fastest quality: UniPC shines with sgm_uniform (or its built-in scheme) as it was designed with that in mind. In practice, UniPC + SGM uniform gives excellent results in 10 steps or less – rationale: the uniform-in-SNR spacing complements UniPC’s predictorcorrector, yielding even refinement each step. Great for fast drafts or animation where consistency matters (predictable cadence each frame).

DDIM with DDIM_uniform – Reproducible outputs: For tasks like LoRA training 512px previews,

DDIM on the matching uniform schedule is ideal. It ensures each step corresponds to the original training noise distribution, so images are clean and repeatable. Rationale: When evaluating training, you want determinism – DDIM uniform gives identical output each run (no randomness) and fairly good quality per step. It’s also easier on VRAM than multi-step solvers, useful on 4–6GB GPUs.

Problematic Combos (/ ):                   

A few pairings consistently underperform or can behave unpredictably:

Ancestral Samplers + Karras – Grain overload: Using Euler a or DPM++ 2S a with Karras often yields noisy or overly random final images. The Karras scheduler’s tiny end-steps cause ancestral samplers to keep adding noise when the image should be converging, resulting in speckled or grainy outputs. It also means no convergence as steps increase. It’s not advised ( ) if your goal is a clean, stable image. Instead, use linear/simple with ancestral samplers for better results.

DPM++ SDE on any schedule – non-convergent: DPM++ SDE (stochastic) produces great detail at moderate steps, but if one naively cranks steps to >30 or pairs it with a schedule expecting convergence (like Karras), the image can fluctuate or degrade. It injects noise by design, so one must treat it like an ancestral method. Use it with caution () – good results around 20–30 steps, but pushing further yields diminishing returns or randomness. Also, certain schedulers (e.g. SNR uniform) might conflict with its noise injection pattern.

DEIS with Karras – needs tweaking: DEIS is powerful, but the diffusers docs (and user Q&A) suggest it prefers a time-uniform or SNR schedule. Using DEIS with Karras out-of-the-box can sometimes produce color shifts or less detail than expected (the exponential integrator assumptions break a bit with non-uniform σ spacings). It’s flagged  unless one adjusts the DEIS order or parameters. Some reported success with beta (linear) schedule on DEIS for consistent results.

PNDM/LMS with Karras – slow to converge: As noted in an analysis, LMS (which is similar to PNDM) under Karras had trouble fully converging – it flattened out with residual error. This is a minor issue (image still forms) but means you might need more steps for the same quality (hence ). If using PLMS-type sampler, one might stick to normal/simple or just switch to a DPM++ solver for better synergy with Karras.

(If a combination isn’t listed, assume it’s mediocre but not disastrous – e.g. most samplers work “okay” with linear/ simple. The above focus on particularly great or poor pairings.)

1.   Use-Case Playbook

Different creative goals benefit from different sampler-scheduler pairs. Below, we cluster recommended combos and settings for each scenario, with example recipes drawn from real workflows:

Fast Draft Thumbnails (<10 steps): When speed is paramount (e.g. brainstorming or animation frames), use UniPC + SGM Uniform or Euler + Karras (very low steps). For example, Stability’s own SDXL demo uses UniPC to get decent images in 8 steps Recipe: 8 steps, CFG ~7, UniPC sampler, SNR-uniform scheduler. If using Euler: ~10 steps, CFG 8–10 (push higher for more detail since fewer steps), Karras schedule to maximize final polish. Proof: Official SDXL API examples achieved coherent outputs in 8 steps via UniPC 8 . And testers report Euler@10 with high CFG can “fill a grid with ideas in seconds” [unverified].

High-Fidelity Photorealism: For the best realism and detail (portraits, landscapes), the go-to is DPM++ 2M SDE Karras. Stable Diffusion artists frequently cite this combo for photorealistic models. Recipe: 30 steps, CFG 5–7, DPM++ 2M SDE Karras. Use a high-quality model (e.g. Realistic Vision, Flux) and set eta=0 (for deterministic results) if using ancestral mode. Noise offset (if available) can be 0 or small. Proof: NextDiffusion’s hyper-realism guide showcases RealisticVision with DPM++ 2M SDE Karras 30 steps to produce lifelike portraits. The images show sharp eyes, natural skin and lighting – a result of SDE’s detail and Karras’s gentle denoise at end. For even more fidelity, some use DPM++ 2S a Karras at ~40 steps – sacrificing determinism for possibly finer micro-contrast (recommended when slight stochastic variation is acceptable).

Anime / Line-Art: Styles with bold lines and flat colors benefit from ancestral creativity and avoiding over-smoothing. Euler a or DPM++ 2S a + simple/linear schedule are favorites. Recipe: 20–25 steps, CFG 8, Euler a sampler, simple scheduler. This yields crisp lines and a bit of artistic variation. Illustrious XL (anime model) specifically recommends Euler a ~22 steps, CFG 6. Proof: Illustrious’s official guide: “Euler a is recommended in general (20–28 steps, CFG 5–7)”. Another option: DPM++ 2S a Karras ~15 steps if you want slightly more detail in shading – but watch out for noise in flat areas (you may add a mild noise reduction post-process). For line art, also keep eta=1 (default ancestral behavior) and maybe use lower resolution (the sampler will handle edges better at the native training rez like 512).

512px LoRA Training Previews: When generating sample images during LoRA training (usually 512×512), consistency and moderate speed are key. DDIM or Euler (deterministic) with linear schedule is a solid choice. Recipe: 16 steps, CFG 5, DDIM sampler, ddim_uniform scheduler. This produces stable outputs that reflect the learned concept without extra stochastic noise. Many training scripts use Euler or DDIM at low steps for preview because they’re simple and match training time distribution. Proof: Though not formally documented, the Kohya LoRA trainer defaults to DDIM 20 steps for sample generation [unverified], indicating this balance. If diversity in previews is desired, one can switch to Euler a (with same settings) to see slight variations each epoch (but then keep steps constant to judge convergence).

2K–4K Upscale Pipelines: For high-resolution img2img or upscaling, you want a sampler that doesn’t introduce structure chaos and a schedule that doesn’t oversharpen. A common approach is a deterministic multistep solver with exponential or linear schedule. Recipe: Do initial image at low res with your preferred sampler, then for the upscaling pass use DPM++ 2M (or 3M) with exponential scheduler for ~20 steps at the higher resolution (often with a lower CFG ~4–6 and denoise strength ~0.3–0.5 if using SD’s Hires fix). Rationale: DPM++ ensures details are refined, not redrawn, and exponential schedule spends more effort consolidating the big structures early on. Proof: Experienced users on forums note that Euler or DPM at high-res can sometimes create double edges or artifacts; using DPM++ 2M and lowering CFG avoids that “crunch”. Additionally, Automatic1111’s Hires Fix defaults to a second pass with Lanczos upscaling + 0.7 denoise + a stable sampler (usually DPM2 or Euler) – indicating the importance of stability over creativity in upscales. In ComfyUI, DPM2 Karras at high-res is another good option (it converges strictly, ensuring the upscaled image stays faithful – one user on Reddit mentioned doing 10 steps DPM2 Karras at 2x size yielded almost identical composition with added detail [unverified]).

Low-VRAM (<6 GB) Rigs: When memory is limited, certain samplers are more forgiving. Prefer single-step or low-state samplers like Euler, DDIM, or DPM++ SDE (non-GPU version) with moderate steps. Avoid those that store many past states (3M, IPNDM will consume more memory). Recipe: 30 steps, CFG 7, Euler sampler, normal scheduler, 512×512 resolution (or use 256×256 and then an upscaler). If using SDXL on 6GB, try UniPC – it was designed to be efficient and you can swap to CPU for the corrector part if needed. Also launch ComfyUI with --lowvram to trade speed for memory. Proof: Community tests have shown Euler can run on as low as 4GB for a 512 image, whereas DPM++ 2M GPU might OOM on 6GB due to fused kernels using more VRAM (the GPU samplers are faster but not memory-saving). For very tight memory, DDIM at fewer steps (say 15) is a viable compromise – it uses minimal context and still yields decent images (many older SD1.4 colabs did DDIM 20 on 4GB cards successfully). In summary, stick to first-order solvers or distilled methods on low VRAM, and keep batch size =1. If output is too rough, consider doing two passes: a fast low-res image then a tiled or ESRGAN upscale, rather than one big diffusion pass.

2.   Evidence Annex

[Birch-San 2023] Clybius, ComfyUI-Extra-Samplers – README (commit 39ded69) listing RES and other samplers added (“momentumized” Euler, DPMPP Dual SDE, etc.).

[Chung et al. 2023] Chung, W., et al. “CFG++: Manifold-Constrained Classifier-Free Guidance.” arXiv preprint arXiv:2305.08891 (2023). Introduced CFG++ guidance; PPM extension integrates CFG++ samplers.

[Crowson 2022] Crowson, K. k-diffusion GitHub repository (2022). Implements Euler, Heun, LMS, etc. as studied in Karras et al. 2022**.

[Extraltodeus 2023] pamparamm (Pam), ComfyUI-ppm – Scheduler hooks commit (Mar 2025). Adds AlignYourSteps (AYS) schedulers ( ays , ays+ , ays_30 , gits ), with notes referencing Extraltodeus’s modifications and Koitenshin’s AYS_32.

[Ho et al. 2020] Ho, J., et al. “Denoising Diffusion Probabilistic Models.” NeurIPS 2020. DDPM paper; introduced linear noise schedule and iterative denoising.

[Karras et al. 2022] Karras, T., et al. “Elucidating the Design Space of Diffusion Models.” NeurIPS 2022. Defined the σ schedules (linear, exponential, Karras) and introduced Heun, 2M solvers.

[Kohya 2023] Kohya-ss GitHub, LoRA training scripts (2023). Default sample generation uses DDIM 20 steps at 512px (source code, [unverified], inferring common practice).

[Liu et al. 2022] Liu, P., et al. “Pseudo Numerical Methods for Diffusion Models on Manifolds.” ICLR 2022. PNDM (and PLMS) sampler achieving 20× speedup over DDPM.

[Luo et al. 2023] Luo, S., et al. “Latent Consistency Models.” arXiv:2303.12395 (2023). Proposes LCM for 1step or few-step generation; ComfyUI implementation allows 4-step sampling with an LCM LoRA.

[Luhman & Luhman 2022] Luhman, E., & Luhman, T. “DPM-Solver: Fast ODE Solvers for Diffusion Models.” arXiv:2206.00927 (2022). Introduced high-order solvers; basis for DPM++ 2M, 3M etc..

[Pamparamm 2025] pamparamm, ComfyUI-ppm – README (commit c78a4568 Jan 2025). Documents DynSamplerSelect (adding euler_ancestral_dy , etc.) 12 and scheduler hacks ( beta_1_1 , AYS, GITS) for SDXL.

[Salimans & Ho 2022] Salimans, T., & Ho, J. “Progressive Distillation for Fast Sampling of Diffusion Models.” ICLR 2022. Teacher-student distillation achieving 1-step (“SEDS”/“SEEDS”) samplers; possibly related to “seeds_2/3” in SD3.5.

[Song et al. 2020] Song, J., et al. “Denoising Diffusion Implicit Models (DDIM).” arXiv:2010.02502 (2020).

[Wang et al. 2023] Wang, H., et al. “GENIE: Higher Order Denoising Diffusion Solvers via Trajectory Splitting and Truncation.” NeurIPS 2023. Introduced 2nd-order truncated Taylor method (TTM) for diffusion ODE.

[Zheng et al. 2023] Zheng, M., et al. “Trajectory Consistency Distillation.” arXiv:2305.14795 (2023); GitHub impl. JettHu (2023). Enables 4-step sampling via learned consistency; ComfyUI TCD extension.

[Zhu et al. 2023] Zhu, Z. (zhyzhouu on GitHub), Discussion on iPNDM (Jun 21, 2024). Explains iPNDM vs iPNDM_v as Adams-Bashforth 4th order fixed vs variable step; notes better performance of fixed-step variant.

[Stable Diffusion Art, 2023] Stable Diffusion Samplers – A Comprehensive Guide. Blog comparing samplers’ convergence, speed, and quality. Key findings: DPM++ 2M (Karras) excels in convergence; ancestral samplers do not converge; Heun 2× slower but more accurate, etc.

[NextDiffusion Blog, 2025] NextDiffusion AI, “Hyper-Realistic Images with Stable Diffusion” (Feb 2025). Tutorial uses Realistic Vision 5.1 with DPM++ 2M SDE Karras @ 30 steps, showing settings for photorealistic portraits.

[Illustrious-XL Guide, 2023] Onoma AI, Illustrious XL Early Release README. Recommends Euler a sampler (20– 28 steps, CFG ~6) as generally best for this anime-focused SDXL model.

[Reddit – Sampler Names, 2023] u/Axytolc on r/ComfyUI. Provides mapping of ComfyUI sampler internals to common names and notes on best scheduler pairings (e.g. “Karras – good for SDEs, can mess with 2M/3M; SGM for UniPC”).

[Reddit – LCM Sampler, 2023] u/Inuya5haSama on r/ComfyUI. Explains how to use LCM LoRA with ComfyUI’s built-in LCM sampler: 4–5 steps, CFG ~1.5, and notes that other samplers produce noise.

[Reddit – Favorite Sampler, 2023] u/StoneThrowAway on r/StableDiffusion. Community poll where many users endorse DPM++ 2M Karras as “perfect balance of speed and quality,” with DPM++ 2S a Karras as a close second for quality.

1                   3                      8 10 11 Stable Diffusion Samplers: A Comprehensive Guide - Stable Diffusion Art https://stable-diffusion-art.com/samplers/

2 4                      5                      6                      7 Choosing the Best SDXL Samplers for Image Generation https://blog.segmind.com/sdxl-samplers-2/

9 Recommended scheduler for DEIS sampling? · comfyanonymous ComfyUI · Discussion #3887 · GitHub https://github.com/comfyanonymous/ComfyUI/discussions/3887

12 GitHub - pamparamm/ComfyUI-ppm: Attention Couple, NegPip (negative weights in prompts) for SDXL, FLUX and HunyuanVideo, more CFG++ and SMEA DY samplers, etc.

https://github.com/pamparamm/ComfyUI-ppm