1. 介绍

本文将尽量通俗地介绍扩散模型训练中，高级训练参数的原理和效果。本文为笔记性质的文章，旨在与读者一同学习，并帮助读者对这些拗口名字的参数有基本的认识。本文不会涉及任何复杂的数学推理，对数学原理感兴趣的同学可自行查阅相关资料。

2. 前置知识

本节将介绍扩散模型的基本概念，帮助读者对扩散模型有基本的科学认知。本文将默认读者已经了解一些更基本的计算机知识，例如计算机储存图像的方式等。

2.1. 扩散模型

2.1.1. 什么是扩散模型？

扩散

扩散模型是目前最常见的图像生成模型的底层架构，如 Stable Diffusion，NovelAI Diffusion V3 等模型均属此类。科学家从墨水滴入烧杯中逐渐扩散开的热力学现象中获得了启发。墨水从墨滴逐渐扩散，与水混合成为溶液，是一个从有序到混乱的过程，这与绘画从起草到成图的过程类似，不过是后者是从混乱到有序的逆过程。墨滴能自发地溶解为溶液，您也能够轻而易举地涂改破坏艺术作品，却难以分离墨和水，也难以重构一幅绘画作品——破坏有序容易，恢复有序困难。

扩散中的信息熵

理解扩散模型中的信息和噪声非常重要。从信息的角度看，有序代表信息，而无序代表噪声。在图像处理中，噪声指的是画面中混乱无序的部分，如损毁的相片。布满噪声、完全嘈杂的图像称为白噪声，如老式电视的雪花。

图像中的噪声与信息是两个互补的概念，噪声越多，图像越嘈杂，图像中的信息越少；噪声越少，图像越干净，图像中的信息越多。信息与噪声的比值称为信噪比（signal-noise-ratio），简称SNR。墨滴状态的墨水和完成的绘画作品，信息多，噪声少，信噪比最高（=正无穷）；而溶液状态的墨水和刚起草的画稿，信息少，噪声多，信噪比最低（=0）。

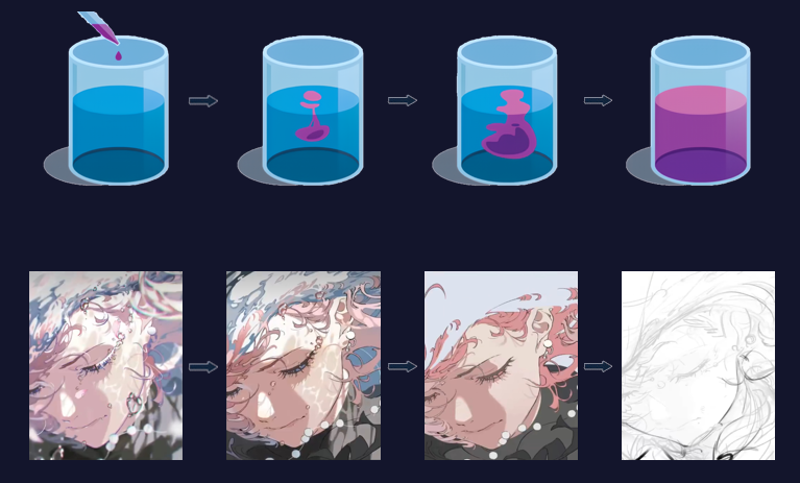
正向扩散和逆向扩散

如上文所述，秩序的破坏比恢复更加容易，而AI的特性是从经验中学习。科学家让AI观察信息被摧毁，噪声被引入的过程，并以此为经验学习消除噪声，重建信息。

其中，摧毁信息、添加噪声、信噪比逐渐降低的过程称为前向扩散（forward diffusion），而消除噪声、重建信息、信噪比逐渐升高的过程称为逆向扩散（backward diffusion）。模型从正向扩散中学习知识（训练），于逆向扩散中应用所学的知识（推理）。

扩散模型图像生成

扩散模型的训练开始于一张无任何噪声的干净图像x0，记初始时刻为t=0，每过一个单位时间，就通过向图像中添加一定比例噪声的方式摧毁图像中的一部分信息。随着时间的增加，图像愈发嘈杂，直到大量的噪声完全淹没了图像中的所有信息，图像称为白噪声，记此时的时间为t=T，白噪声图像为xT。

如此一来，在正向扩散中，每一张图像都对应一个白噪声。在学习了足够多白噪声与图像的对应关系，摸索出制造白噪声的规律后，模型便能够通过任意一个白噪声“猜测”出它大致对应的图像了，即使这个模型并没有见过白噪声，它也能应用自己学习掌握的规律来达成。

逆向扩散逆转了正向扩散的过程。为了逆转时间，它设定当前时间为正向扩散中白噪声产生的时间t=T，并将白噪声命名为x'T，并开始逐渐地，每经过一个单位时间，从x'T中移除一定比例的噪声。最终，随着一点点噪声被移除，白噪声被“还原”为了原始图像，称为x'0，即最终生成的图像。

其中描述的时间并非真实物理意义上的时间，而是对物理热力学扩散过程的比喻。每一个加噪和去噪的时间节点称为一个时间步（timestep）。

正向扩散通常包含1000个时间步，要在逆向扩散中完整模拟每一个时间步下的降噪非常耗时。而由于模型已经掌握了足够丰富的知识，充分了解了自己在重建图像的每一个时间步时应该移除多少噪声。因此，只需要从完整的几个时间步中抽取其中几个（通常是20~40个），便足够模型消去足够的噪声了。抽取哪几个时间步由采样器（sampler）决定，如 Euler A，DPM 2M，DDIM等。

提示词引导的图像生成

为了引导扩散模型生成具有指定内容的图像，训练图像需要有一段标注（caption）来描述其画面内容。标注将与图像一同传入扩散模型，以关联二者。

2.1.2. 扩散模型的结构

扩散模型的模块

扩散模型并不是一个单一的简单模型，而是由多个部分构成的复杂模型，每一个部分称为一个模块（module）。一个常规扩散模型的基本模块有：

• UNET：扩散模型最主要的结构，也是训练和微调的主要对象，用于在给定嘈杂的图像xt和当前时间t时，预测x(t-1)，即前一个时间步的图像。具有这种功能的网络结构能够替代 UNET，例如被证明效果更好的 ViT 和 DiT。

• Text Encoder：文本编码器，关联文本和图像，能够在微调中训练。

• VAE：图像编码器，能提取图像中关键和易于识别的主要特征，将图像压缩（编码）入潜空间（latent space）称为潜变量（latent variable），或将潜变量解压（解码）回原本的图像。VAE 能极大地减小图像尺寸，加快模型的处理速度。使用了 VAE 的扩散模型称为潜在扩散模型（latent diffusion model）。

• Tokenizer：分词器，用于将文本提示词翻译为词元（token），进而处理为模型能够接受的数字输入，或称为文本嵌入（text embedding）。

2.1.3. 正向扩散

正向扩散过程逐步向图像中添加噪声，其本质是，每经过一个时间步，就随机生成一个与图像等大的高斯分布噪声，按一定比例与这一时刻的嘈杂图像相混合。时间经过的越久，图像越嘈杂。另外，每一时刻添加噪声的量和形状也不同。随着时间步增加，添加高斯噪声的均值逐渐减小，而方差逐渐升高。直到最后，图像会完全嘈杂，成为一片白噪声，服从均值为0，方差为1的标准高斯分布。

为了衡量加噪加到 t=t 时刻嘈杂图像中噪声的量和形状，我们引入变量 αt 和 σt 来表示特定时刻注入噪声的均值和标准差。根据论文作者复杂的数学推理，αt 与 σt 的平方和会始终等于 1。αt^2 会随时间步增加而原来越小，而 σt^2 = 1 - αt^2 会越来越大，二者平方的比值就是前文提到的信噪比 snr(t) = αt^2 / σt^2。

2.1.4. 逆向扩散

噪声预测

逆向扩散即是模型推理。逆向扩散从一张随机生成的白噪声图像开始，逐步从白噪声中消除一定比例的噪声，最终逐渐获得清晰完整的图像。这一过程可简化为，当接收到任意一张嘈杂的图像时，模型必须能够预测出该嘈杂图像去噪后的原图，无论该图像有多么嘈杂。而另一个附加的输入——时间步 t，还会告诉模型图像的嘈杂程度，以辅助去噪。

由于模型在正向扩散中已经具有摧毁原始图像来获取其对应白噪声的能力，因此，让模型预测去噪后原图的任务，其实等价于让模型预测嘈杂图像完全加噪后白噪声的任务。经过数学推理，这种转化等价于：预测原图的损失函数 = snr * 预测白噪声的损失函数。这里，损失函数是机器学习里的重要概念，衡量了模型预测的值和真实值之间的差距。

要让这种转化发生在生成中则在数学上困难得多，本文不做赘述，感兴趣的读者可参阅 扩散模型 Diffusion Models - 原理篇 - 知乎 (zhihu.com)。转化后，虽然最终目的一致，但模型的表面任务变为了预测白噪声而非原始图像，因此，这种预测方式被称为噪声预测（noise prediction）。

为了完成这一噪声预测任务，逆向扩散需要从正向扩散中学习有关噪声分布规律的知识。具体的学习方式为，训练的每个步骤中，按照以下步骤操作：

1. 抽图：从数据集中抽取一张图像 x0；

2. 抽时间步：随机抽取一个0~1000之间的整数 t ∈ [0, 1000]，作为要学习的时间步；

3. 加噪：向 x0 中添加均值为 αt，标准差为 σt 的高斯分布噪声 ε，获得 xt；

4. 预测：将 xt 和 t 输入模型，让模型生成他认为 xt 所对应的白噪声，记为 ε'；

5. 计算误差：计算真实噪声 ε 和预测噪声 ε' 之间的误差大小，记为 L；

6. 更新权重：通过机器学习方法，让模型朝着缩小 L 的方向学习，即更新自身的权重值。

3. 正文

3.1. V-预测 V-Prediction

V-预测（V-Prediction）是噪声预测以外的另一种模型预测方式。其名“V-预测”中的 “V” 指的是 Velocity，即速度。那么，预测的是什么的速度呢？要搞清楚这个问题，我们需要回到前文。从 2.1.3. 正向扩散中，我们学到，模型第 t 时间步相比于原图的加噪量服从均值为 αt，方差为 σt 的正态分布，且满足 αt^2 + σt^2 = 1，这像极了三角函数中 sin(φ)^2 + cos(φ)^2 = 1。因此，把 αt 和 σt 分别看做 sin(φ) 和 cos(φ)，那么正向扩散中所加噪声从 (α0=1, σ0=0) 到 (αt=0, σt=1) 的变化就相当于单位圆上的向量 z=(αt, σt) 从纵轴转向横轴的变化，切线为速度 v，即如下图所示：

因此，V-预测中的速度，实际指的是所加噪声变化的速度。经过数学推导，预测这一速度同样能等价于预测原图，唯一不同的是V-预测损失函数前额外乘以的系数，即：V-预测的损失函数 = (snr + 1) * 原图预测的损失函数。

结合上文原图预测与噪声预测之间的转化公式，就得到了原图预测与V-预测之间的关系：V-预测的损失函数 = (snr + 1)/snr * 噪声预测的损失函数。

对比V-预测和噪声预测同原图预测之间的转化关系，不难发现，当时间步 t=T 时，信噪比 snr(T) = 0，这时的噪声预测的损失恒定为 0，模型无法从中学习。但V-预测通过给系数 snr 加上了 1，变为 (snr + 1) 避免了 snr 在任何时间步等于 0。这看似简单直观的修改，却改善了训练。

更多关于V-预测的数学推导请参见：扩散模型中的v-prediction - 知乎 (zhihu.com)

论文原文：[2202.00512] Progressive Distillation for Fast Sampling of Diffusion Models (arxiv.org)

3.2. 零端信噪比 Zero Terminal SNR

见： 【科普】为什么你的模型无法生成很暗或很亮的图像？ | Civitai

3.3. 最小信噪比 Min SNR Gamma

最小信噪比（min snr gamma）的提出是为了解决一个不易察觉的训练缺陷。为了理解这一缺陷，我们需要回顾损失函数的效用。在机器学习中，损失函数衡量预测值与真实值之间的差距。模型会根据损失函数计算出的差距来更新自身权重。差距越大，模型认为自己距离真实值越远，因此越倾向于向真实值的方向变动。

在通常的扩散模型训练中，不同时间步损失函数的权重相同，模型的预测与真实间的误差不受时间步 t 干扰。但是，不同时间步之间的训练其实会相互干扰，例如，第 100 时间步学到的知识会干扰到第 500 时间步的知识。为了更直观的理解，我们不妨将整个任务细分为 1000 个各自独立的学习任务，在第 t/1000 个任务中，模型被要求专门地去噪第 t 时间步的嘈杂图像来生成原图。可是在训练中，模型的权重只有一份，且每经过一个训练步骤都会更新一次。然而，在训练中，我们训练的是一个特定的时间步，从 0~1000 之中抽取。这种不同时间步之间的知识的相互干扰会阻碍模型的学习，模型需要很久很久才能逐渐学会与这 1000 个子任务和睦相处。

然而，要从数学上解决这样一个同时优化所有子任务的问题是很困难的，需要消耗大量的算力才能解决，最终反而可能拖慢了训练。因此，作者选取了一个替代方案，即最小信噪比策略。该策略将原本的损失函数变为：最小信噪比的损失函数 = min(snr, γ) * 原图预测的损失函数。其中，γ 为人为设定的常数值，默认为5。

与噪声预测的损失函数相比，最小信噪比的损失函数乘以的系数是 min(snr, γ) 而不是噪声预测里的 snr。由于信噪比 snr(t) 随时间步 t 从正无穷逐渐降为 0，因此，最小信噪比损失函数的系数约束了低时间步下损失函数的权重，本质上是限制了模型去集中于学习过小的噪声细节。

这一使模型训练的收敛速度提高到了原先的 3.4 倍，如下图所示：

论文原文：[2303.09556] Efficient Diffusion Training via Min-SNR Weighting Strategy (arxiv.org)

3.4. 整改流 Rectified Flow

整改流（Rectified Flow），简称 RF，是 Stable Diffusion 3 论文应用的有效方法之一。该方法通过修改训练时对时间步的采样方式从等概率随机抽取，来提高中段时间步被抽取的概率。

观察过图像生成过程的同学应该能发现，对图像结构起重要作用的的采样步骤往往是中间一段，这对应着中段的时间步。为了在训练中能更多地考虑到这些有重要作用的时间步，SD3 通过将时间步的采样分布从均匀分布更改为逻辑正态分布而取得了令人满意的的结果。这里，逻辑正态分布可简单理解为更易控制和灵活的正态分布，受两个参数m和s表示。m表示波峰位置，s表示方差，二者对分布结果的影响效果如下图所示：

但是，RF 的应用也改变了模型的加噪方式，因此并不能用于微调中。

原文地址：[2403.03206] Scaling Rectified Flow Transformers for High-Resolution Image Synthesis (arxiv.org)