Demystifying SNR (Min SNR, Debiased Estimation, and IP Noise Gamma)

Motivation:

I recently was playing around with loss and SNR and I wanted to make a publicly available resource for talking about SNR (both on a basic level and at a medium depth level). Many tutorials and explanations doesn't cut it for me because they're often hand-wavy, go on a tangent, say it's too long to explain (when it's not), and or all of the above; then when we go read advanced research papers, they don't have basic graphs for SNR and transformation proposed in their paper, which is sometimes frustrating.

I will also explain what is actually happening in min SNR, Debiased estimation, and IP noise gamma in Kohya (for lora and checkpoint training). I will also attach a basic python file for the calculations I did.

I will be referencing some papers for respective algorithm/techniques by the following names. They're not necessary to read, but I'll list them for like-minded people that wants them, and please feel free to correct me if I misinterpret or get something wrong in this article.

- Min-SNR paper: https://arxiv.org/pdf/2303.09556

- Debias SNR paper: https://arxiv.org/pdf/2310.08442

- IP gamma paper: https://arxiv.org/pdf/2301.11706

Quick and dirty refresher for SNR by chatGPT-4o (in blue):

Understanding SNR in SDXL:

In SDXL, SNR (Signal-to-Noise Ratio) plays a crucial role in determining the quality and clarity of the generated images. Think of SNR as a measure of how much useful information (signal) is present in your image compared to the unwanted random data (noise). A higher SNR means your image will be clearer and more detailed, while a lower SNR means it might be grainier and less distinct.

- min_SNR: This parameter sets the minimum acceptable SNR for your images. By adjusting min_SNR, you can control the baseline quality of your generated images. If you set it too low, you might end up with images that are too noisy. Set it higher, and you ensure a better quality, but it might also slow down the generation process.

- ip_noise_gamma: This parameter influences how noise is added during the image generation process. By tweaking ip_noise_gamma, you can balance between smooth gradients and detailed textures. A higher value can help in reducing noise, leading to smoother images, while a lower value might retain more texture detail but also more noise.

SNR in SD1.5 vs. SDXL:

One important thing to note is how SNR differs between SD1.5 and SDXL. SDXL is a latent model, meaning it works in a compressed latent space rather than directly with pixel data. This means the way SNR impacts image quality is slightly different. In SD1.5, SNR directly affects the pixel-level details and noise, while in SDXL, SNR impacts the latent space representations before being decoded into the final image. As a result, adjusting SNR and related parameters in SDXL can have a more nuanced effect on the final image quality, often allowing for more refined control over noise and detail.

That's it from chatGPT, from here, it's my rant.

What is a diffusion model:

All stable diffusion models (1.5, XL, etc) are at it's core a diffusion model that relies on adding noise (forward process) to the original data and making a model learn to denoise (backward process).

Timestep:

If you trained a Lora for stable diffusion, you probably seen the min and max timestep, usually 0 and 1000 respectively. This is the widely adopted timestep for training a diffusion model (cause the original paper did it and it's adopted in SD).

One interesting fact that is well known is that the model's strategy on how to denoise changes depending on t, which makes sense as the model needs to first denoise a general composition in the high t range (prob t > 600), then move on to generate smaller details and textures (t roughly between 200~500). Many papers touch on this problem where the model's denoising strategy is different depending on specific timestep ranges, but the default setting is true to the original paper and doesn't do anything special to address this. The different SNR strategies (Min SNR and Debiased Estimation) and different noise scheduling (IP noise gamma, multi-res noise, etc) are attempts to tackle this problem.

TLDR:

Max timestep, T = 1000

Min timestep = 0

t ∈ [0, T] = [0, 1000]

Here's a table for the base SNR(t) for every 25 timestep, the first column t is actually the index for the timestep list so t=0 is actually the SNR associated for

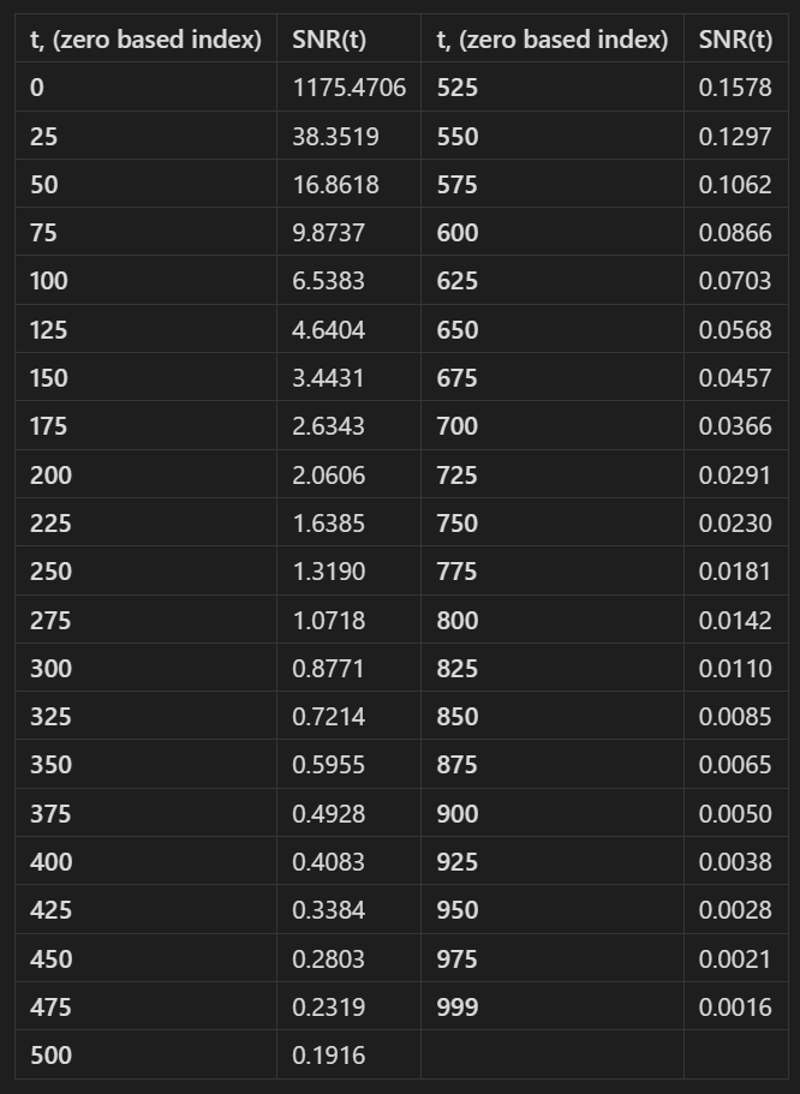
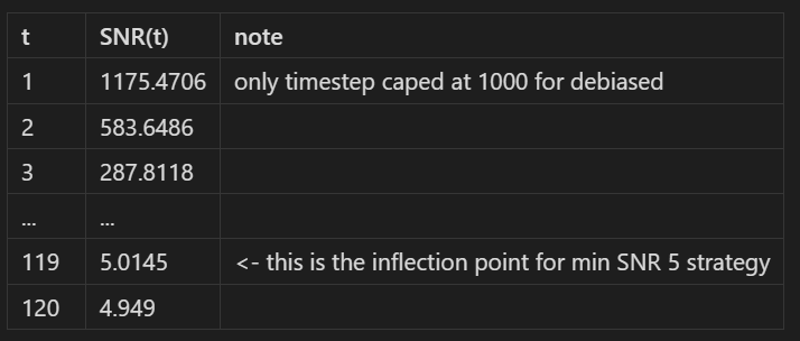
Few additional time, t, that I think is important to note:

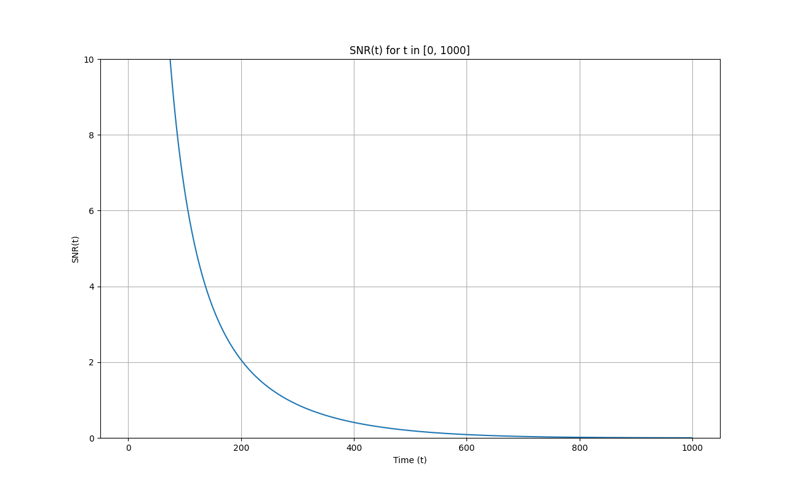
Here's the graph for SNR(t), I cut off values above 10 or else the slope looks flat:

basically SNR is something we can compute beforehand and I think it's nice to have this explicitly stated for this discussion.

## Basic explanation of Min SNR and Debiased Estimation:

Both Min SNR and Debias are methods of adding a multiplier to the loss based on the SNR of the timestep. Both methods are very similar under the hood. Basically they compute a weight based on the SNR and they multiply the loss by the computed weight.

Here's how both Min SNR and Debiased are called in Kohya (I removed the if clauses regarding v-pred in the code cause we don't care about them and we don't enter that condition for SDXL or SD1.5):

loss = torch.nn.functional.mse_loss(noise_pred.float(), target.float(), reduction="none")
loss = loss.mean([1, 2, 3])

if args.min_snr_gamma:
	loss = apply_snr_weight(loss, timesteps, noise_scheduler, args.min_snr_gamma)
# ...
# loss adjustments using v-pred, but we don't care for 1.5 or XL
if args.debiased_estimation_loss:
	loss = apply_debiased_estimation(loss, timesteps, noise_scheduler)

loss = loss.mean()  # mean over batch dimension

Here's how Min SNR works:

def apply_snr_weight(loss, timesteps, noise_scheduler, gamma, v_prediction=False):
    snr = torch.stack([noise_scheduler.all_snr[t] for t in timesteps])
    min_snr_gamma = torch.minimum(snr, torch.full_like(snr, gamma))
    weight = torch.div(min_snr_gamma, snr).float().to(loss.device)
	# if case for v-pred, ...
    return loss * weight

Here's how Debiased Works:

def apply_debiased_estimation(loss, timesteps, noise_scheduler):
    snr_t = torch.stack([noise_scheduler.all_snr[t] for t in timesteps])
    # if timestep is 0, snr_t is inf, so limit it to 1000
    snr_t = torch.minimum(snr_t, torch.ones_like(snr_t) * 1000) 
    weight = 1/torch.sqrt(snr_t)
    return loss * weight 

The weights for min SNR = 5 (lowers the loss for low timesteps):

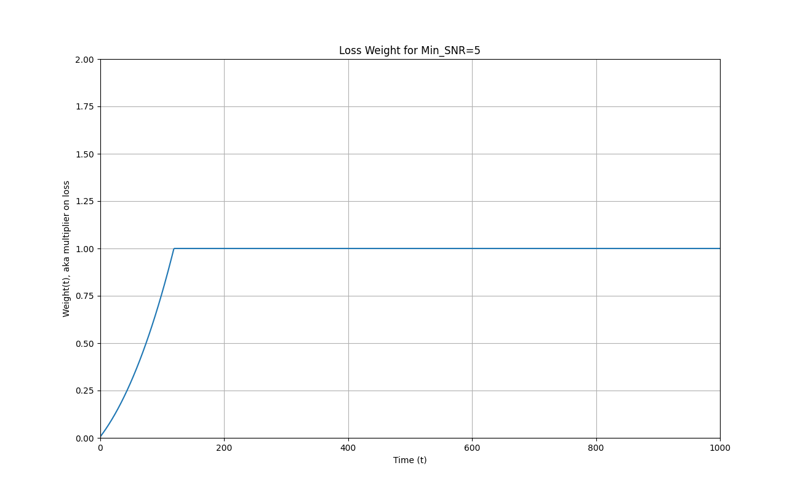
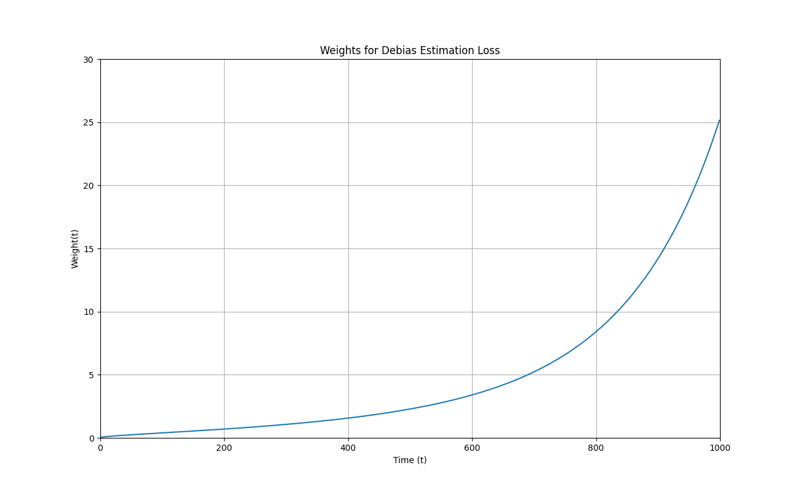
Debias weights (on top of lowering loss for low timestep, it exponentially increases the loss for bigger t):

What happens if we use both:

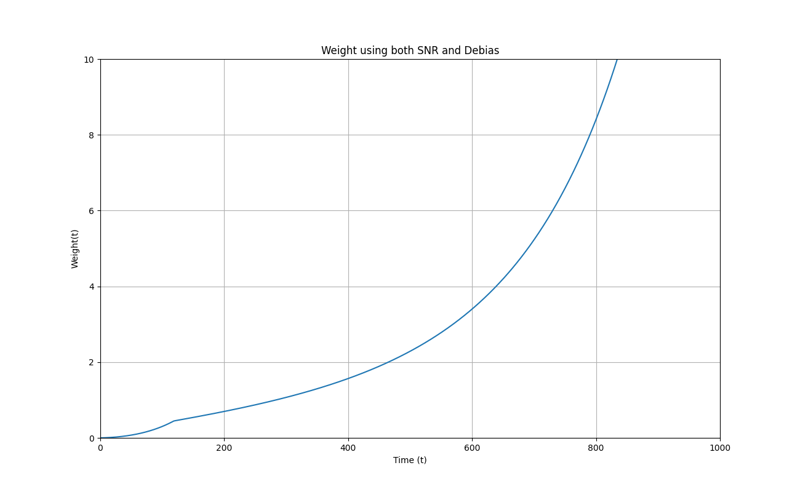
Following Kohya's order of operation, Debias(Min SNR(t)) Not detrimental but you're lowering the loss for the early timesteps twice. There's no reason to have both enabled in this scenario, choose one or the other.

Debias vs Min SNR:

We observed that Debias outputs a slightly better quality lora than the one made with Min SNR strategy. Our observation aligns with the paper's result. The main difference between min SNR and Debias is the range that's affected and if the denominator term is sqrt or not.

IP Noise Gamma:

This paper tackles a different but similar problem. Basically, there's a discrepancy between training and inference, training relies on samples conditioned on the ground truth, while inference relies on previously denoise samples. During training, the model can still "see" the ground truth after the noising process (the degree depends on the sampled t value) because the noise is applied on the ground truth, while during inference, it starts from a truly random noise and there's nothing external that the model can rely on. The paper shows that there's a benefit in adding more noise (perturbing) the ground truth samples to simulate the prediction error.

The original paper suggests using different values for ip_noise_gamma that's timestep dependent, but it adds an extra overhead so they decide to make all ip_noise_gamma terms equal across all timesteps. So they proposed 0.1 as a constant scaling value for the additional noise. A bit reductive and it's sad how they didn't dig deeper in the paper.

This is how it's implemented in Kohya:

# from train_utils.py
noisy_latents = noise_scheduler.add_noise(latents, noise + args.ip_noise_gamma * torch.randn_like(latents), timesteps)

Basically it's adding an extra random noise to the latent on top of the precomputed noise that's scaled to the gamma value, normally gamma = 0.1.

Observation:

The default 0.1 seems to slightly improve the quality of loras compared to ones without it.

We tested values between 0.1 ~ 0.25 and it does seem like 0.1 is the best performing value. (This makes logical sense bc too much noise can be a separate problem).

*Take the following with a grain of salt: (I will update it as I get more info, training checkpoints takes time)

The benefit seems to disappear with checkpoints. This can be because the training procedure is different between loras and checkpoints, where loras are bombarded with a few concepts, while the checkpoint (with large datasets) are trained on random datapoints with shuffled tag. (Note: the checkpoint experiment was with a pony based model, Eclipse XL Ver. 1.3.6, which was trained on booru based tags, so results may differ for different training setup)

Final words

It seems like there's a benefit to loras ditching min SNR and using debiased estimation instead. Also using IP noise gamma on top seems to have good results.

I'm still testing but I will be making character loras, styles, some background, and few other concepts and I'll add more findings to this article.

Additional code to Lora easy trainer:

The settings for debias estimation are in base kohya, but it seems like there's no UI elements in the lora-easy-trainer UI (even on the dev branch) so I added things like debias and I also added a limit feature to the debias's weight here: https://github.com/kukaiN/EasyTrainer_Wasabi_addon feel free to check it out (there may be bugs, I'm just tweaking and logging things as I go).

Updated 7/13/2024